В этой статье я хочу в определенной мере пролить свет на один из часто встречающихся при проектировании гитарных жужжалок моментов и зачастую вызывающий у малоподготовленного человека большие сложности.
Допустим, что Вы собираете не минималистскую грелку, а самостоятельный и самодостаточный (если, конечно, получится)))) ) дисторшн со своим характерным тембром, который будете с собой таскать везде, поражая воображение завистников своим ацким рычанием ну или божественным улюлюканьем - кому что ближе, и может быть даже будете писать его в линию.. Очевидно, что выбрав схемотехнику ограничителя, Вы подойдете к вопросу обэмуляции кабинета. Разумно конечно, предположить, что человек осознанно проектирующий темброблок по заданной АЧХ (или, проще говоря, спикерсим) не нуждается в этой статье. Однако, очень часто схема спикерсима ограничивается одним единственным устройством – фильтром низких частот – ФНЧ (или в буржуйской терминологии Low Pass - LP), а кропотливым проектированием никто не занимается и вообще охота чтобы просто

песок удавить и на том остановиться .

Поэтому рассмотрим несколько вопросов:

· Что такое ФНЧ и зачем он нужен

· Какие бывают ФНЧ

· Схемы ФНЧ и оптимальная элементная база

Итак, что же такое ФНЧ и зачем он нужен? Представим, что мы собрали какой-нибудь ограничитель по элементарной схеме – один операционный усилитель (ОУ) + два встречно-параллельно включенных диода на землю. То есть что-то вроде вот этого: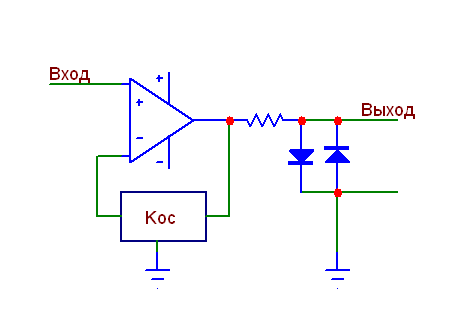

Кос - это блок обратной связи с коэффициентом передачи Кос, который выражает обобщенность структуры - он может быть у всех разный и даже частотно-зависимый. Не имет значения. Включили гитару и подключили это все
куда-нибудь в музыкальный центр или еще круче в компьютер. Дернули за струны и….жужжит, конечно, но жужжит  как-то не эстетично что ли. Да, в звуке очень много так называемого песка (то есть в спектре выходного сигнала присутствует большое количество гармоник высших типов – подали на вход гармоническое колебание с частотой f , а на выходе получили целый букет – сумму колебаний с частотам 2f,3f,…20f и т.д.). Наша задача избавиться от этого песка, не тронув при этом ту полезную часть сигнала, которая нам нужна и еще обязательно пригодится. Однако,сходу возникает вопрос: а где он этот песок начинается? Т.е. начиная с какой частоты (на оси частот в графике спектра сигнала) и выше спектральные составляющие можно уже называть песком? Не вдаваясь особо в
теорию можно смело сказать, что составляющие сигнала с частотами выше 5-6кГц можно смело назвать песком. Приграничная зона - 4-6 кГц – исключительно важная и характер спектра в этой области очень явственно
сказывается на тембре гитарных искажающих устройств. Теперь думаю самое время привести немного поясняющей теории для тех, кто уже напрягся, т.к. в тексте встретились такие понятия как спектр, частота, гармоники и т.д. Рассмотрим взаимосвязи характеристик сигнала на примере гармонического колебания с частотой f=300Гц:

Первое дело – это временная зависимость амплитуды напряжения, т.е. u(t):

Данный сигнал также можно представить и посредством спектрального описания, которое связано с временным преобразованием Фурье, т.е.спектр сигнала – это зависимость величины каждой из составляющих сигнала от частоты. Т.к. сигнал, как и договорились строго монохроматический, т.е. в спектре присутствует только одна спектральная cоставляющая - основная гармоника с частотой f=300Гц и данному сигналу соответствует вот такое спектральное представление:

На слух это воспринимается как ровное спокойное гудение (если громко и долго слушать это монотонное гудение, то можно стать идиотом). А теперь тот же гармонический сигнал подвергнем нелинейному преобразованию, которым и является наша гитарная жужжалка. В результате в весьма упрощенном и обобщенном варианте  зависимость от времени u(t) примет вид: